
Most mathematicians would probably regard the axiom of choice as 'obviously true,' while others may regard it as a somewhat questionable assertion which might even be false( and I am myself inclined towards this second viewpoint). Still others would take it as an assertion whose 'truth' is a matter of opinion or rather, as something which can be taken one way or the other, depending upon which system of axioms and rules of proceedure one chooses to adhere to.

Zorn's "Template"
Let
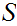 be a Set. Suppose we have defined a "structure" on
be a Set. Suppose we have defined a "structure" on
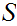 .(I
will not tell you what a structure is). Next, suppose we have a proposition
.(I
will not tell you what a structure is). Next, suppose we have a proposition
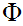 defined on
defined on
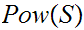 .
.
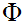 is stated in terms of the structure on
is stated in terms of the structure on
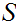 .
.
Restrict attention to
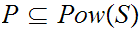 ,
,
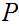 being the subsets such that
being the subsets such that
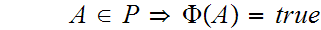
Order
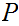 by inclusion of subsets.
by inclusion of subsets.
Prove that if
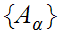 is a chain in
is a chain in
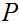 then
then
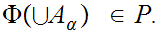
Conclude that there is a maximal element
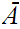
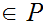 .
That is
.
That is
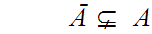
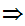
There are discontinuous additive functions -
Discontinuous functions
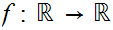 which satisfy the equation:
which satisfy the equation:
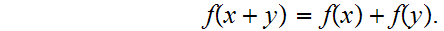
Proof:
Consider
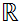 as a vector space over
as a vector space over
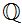 .
Extend
.
Extend
 1
1 to a basis for . We will write it as
to a basis for . We will write it as
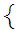 1
1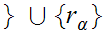 .
Define a map
.
Define a map
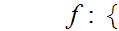 1
1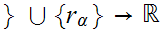
by setting
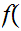 1
1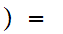 0
and
0
and
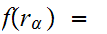 1
for all
1
for all
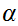 (anything
works as long as one
(anything
works as long as one
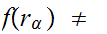 0).
Extend
0).
Extend
 to
all of
to
all of
 , as a map of vector spaces (hence it is additive).But,
, as a map of vector spaces (hence it is additive).But,
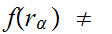 0
for all
0
for all
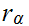 .
Yet
.
Yet
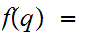 0
for all
0
for all
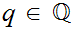 .
This contradicts 19.5.
.
This contradicts 19.5.
There are non-measurable Sets -
A definition of Lebesgue outer measure
A definition of Lebesgue measure
The Banach-Tarski Theorem(Paradox) - It is possible to decompose the 3-sphere " into a finite number of pieces and then reassemble them into two identical 3-spheres using only rigid motions.
Well Orderings of the Reals - Where are they? What is the value of an existence proof?
We begin by reviewing the concepts of consistency and independence of axioms in the context of of Peano's Postulates for arithmetic. We begin with a less-than formal definition of a proof for a system of axioms.
14.1 Very Loose Definitions:
Given a list of axioms
A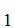 ,A
,A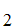 ,A
,A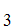 ,......A
,......A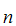
A "proof" of
S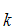 is series of statements and symbols of the form
S
is series of statements and symbols of the form
S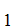 ,S
,S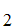 ,S
,S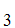 ,......,S
,......,S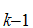
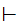 S
S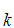 where
each
S
where
each
S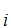 is either an axiom or follows from
S
is either an axiom or follows from
S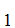 ,S
,S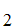 ,S
,S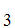 ,......,S
,......,S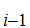 by a rule of inference. We also say
S
by a rule of inference. We also say
S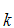 can be proved from
A
can be proved from
A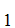 ,A
,A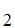 ,A
,A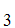 ,......A
,......A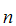 .
.
An example of a rule of inference is Modus Pones
P
,P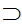 Q
Q
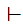 Q
. If P is true and P
impliesQ is true,
then
Q
. If P is true and P
impliesQ is true,
then Q
is true.
Q
is true.
A list of axioms is said to be consistent if there is there
is no statement S for which S
and
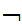 S
(not S) can be proved.
S
(not S) can be proved.
A statement S is independent of
axioms
A ,A
,A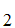 ,A
,A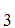 ,......A
,......A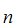 if neither S
nor
if neither S
nor 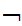 S
can be proved from the axioms. In particular, that the axiom lists
A
S
can be proved from the axioms. In particular, that the axiom lists
A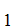 ,A
,A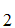 ,A
,A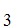 ,......A
,......A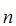 ,S and
A
,S and
A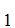 ,A
,A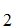 ,A
,A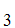 ,......A
,......A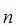 ,
,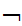 S
are consistent.
S
are consistent.
14.2 Another Loose Definition:
A mathematical model for a list of axioms is a well-defined set which assigns "meaning" for the undefined terms in the axioms, in a manner such that the axioms are "true". The existence of a model proves the consistency of a system since one "knows" that a statement and its negation cannot both be true in a model.
14.3 An Example:
A set
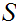 ,
a distinguished element
1
,
a distinguished element
1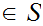 , a a map
, a a map
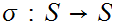 is said to satisfy Peano's Postulates if
is said to satisfy Peano's Postulates if
A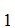 For all
For all
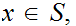
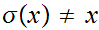
A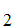 For
all
For
all
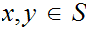
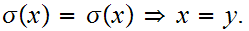
A For all
For all
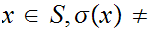 C
C
A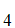 If
If
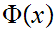 is a proposition such that:
is a proposition such that:
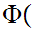 1
1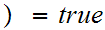 .
.
For all
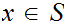 ,
,
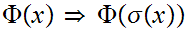
Then For all
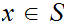 ,
,
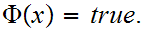
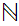 ,
,
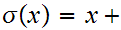 1
is a model for Peano's Postulates. In fact, it is really the only model up to
an appropriate notion of equivalence.
1
is a model for Peano's Postulates. In fact, it is really the only model up to
an appropriate notion of equivalence.
Note that
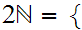 2,4,6,..
2,4,6,..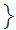 "1"
"1" 2
and
2
and
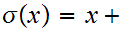 2
also satifies the Postulates
2
also satifies the Postulates
However, Consider the list
A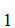 ,A
,A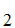 ,A
,A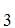 ,A
,A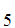 .
.
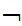 A
A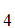 this is consistent since
this is consistent since
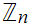 is a model .
is a model .
Thus we can conclude that
A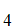 is independent of
A
is independent of
A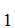 ,A
,A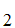 ,A
,A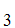 ,A
,A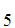 .
.
Let
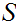 be a set and
be a set and
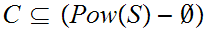 . There exists at least one function
. There exists at least one function
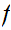
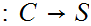 ,
,
such that
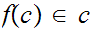
 for
each set
for
each set
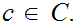
There is no set
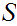 such
that
such
that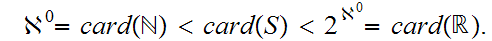
In 1935 Kurt Gödel showed that both AC and CH are consistent with ZF, in
that neither
 AC nor
AC nor  CH can
be proved from ZF. In particular he discovered a model of ZF in which both AC
and CH are true.
CH can
be proved from ZF. In particular he discovered a model of ZF in which both AC
and CH are true.
In 1963, Paul Cohen proved independence AC and CH by first constructing a model of ZF+AC in which CH fails, and then a model of ZF+CH in which AC fails. Together with Gödel's models, this demonstrates that neither the Axiom of Choice nor its negation can can be proved from The Zemelo-Fraenkel Axioms, and that neither the Continuum Hypothesis nor its negation can be proved from Zemelo-Fraenkel Axioms, even in the presence of The Axiom of Choice.