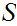 be a given set. Either, for some n there exists a 1 to 1 and
onto function
be a given set. Either, for some n there exists a 1 to 1 and
onto function
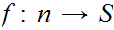 , or there exists a 1 to 1 function
, or there exists a 1 to 1 function
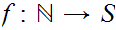 .
.
.
5.1 Lemma:
Let
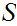 be a given set. Either, for some n there exists a 1 to 1 and
onto function
be a given set. Either, for some n there exists a 1 to 1 and
onto function
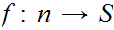 , or there exists a 1 to 1 function
, or there exists a 1 to 1 function
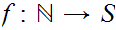 .
.
5.2 Lemma:
Let n
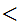 m. There does not exist an onto function
m. There does not exist an onto function
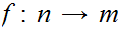 .
There does not exist
.
There does not exist
a 1 to 1 function
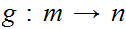 .
.
5.3 Definition: A Set,
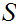 is said to be "finite" if every function
is said to be "finite" if every function
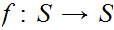 is onto iff it is 1 to 1.
is onto iff it is 1 to 1.
5.4 Theorem:
Suppose I have two finite sets
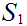 and
and
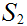 and 1 to 1 maps
and 1 to 1 maps
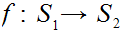 and
and
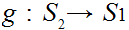 , then
, then
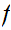 and
and
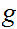 are also onto.
are also onto.
5.5 Theorem:
The following three statements are true:
The subsets
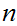 are finite.
are finite.
There exist functions
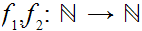 such that
such that
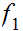 is 1 to 1 but not onto and
is 1 to 1 but not onto and
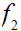 is
onto but not 1 to 1.
is
onto but not 1 to 1.
Let
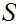 be a finite set, then there exists an
be a finite set, then there exists an
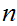 and a 1 to 1 onto function
and a 1 to 1 onto function
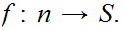
6.8 Theorem:
a. Given
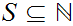 , for any
, for any
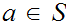 ,
,
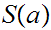 is
finite.
is
finite.
Moreover,
b. either is finite or for any integer n
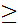 0
we can find a unique
0
we can find a unique
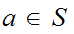 with
with
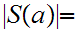 n.
n.
Hence,
c. There exists an order isomorphism
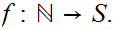
6.9 Theorem:
Let
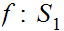
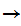
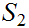 be an order isomorphism. . Then
be an order isomorphism. . Then
1. for all
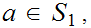
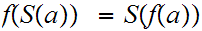
Suppose
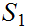 (or
(or
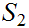 )
is Well Ordered
)
is Well Ordered
2. so is
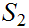 (or
(or
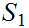 )
)
6.10 Theorem:
For any
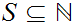
1. There exists an n such that
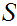 and an order isomorphism
and an order isomorphism
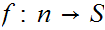
or
2. There exists an order isomorphism
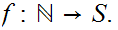
More Examples , Calculations, and Observations:
Define
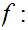
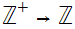 by the formula
by the formula
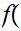 n
n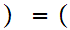 -1
-1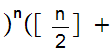 r
r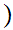
where
n
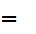 2
2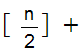 r,
(division by 2 with remainder r ).
r,
(division by 2 with remainder r ).
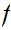 is one to one and onto.
is one to one and onto.
Check
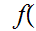 0
0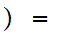 0
0
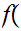 1
1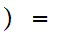 -1
-1
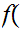 2
2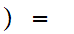 1
1
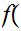 3
3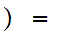 -2
-2
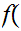 4
4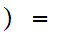 2
2
and so on.
Define
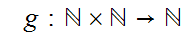 by
the
formula
by
the
formula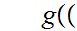 m,n
m,n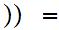 2
2 3
3 again,
again,
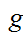 is
one to one. Letting
is
one to one. Letting
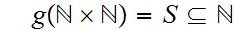 , we can apply 6.10 to find an order isomorphism
, we can apply 6.10 to find an order isomorphism
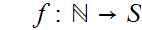 giving
giving
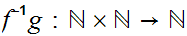 which is one to one and onto. It is not
which is one to one and onto. It is not
an order isomorphism!
One can actually get an explicit map
We want to compare the nature of the previous two calculations.
Define a binary relation
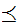 on
on
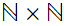 as
follows
as
follows
 m,n
m,n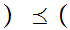 m',n'
m',n' iff
(m
iff
(m 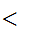 m')
or (if
(m
m')
or (if
(m 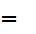 m')
then
(n
m')
then
(n 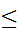 n'))
n'))
Check that this is an Order. It is called "Alphabetic Order"
Here is a picture of Alphabetic Order.
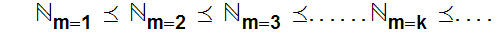
It is also a Well Order!
Proof:
We use the projection
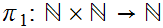 where
where
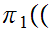 m,n
m,n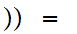 m.
m.
Given a
non-empty
 , consider
, consider
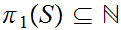 and let
and let
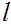 be its least
be its least
member.
Check that every member of
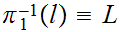 is strictly less than every member
is strictly less than every member
of
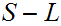 since
since
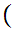 m,n
m,n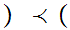 m',n'
m',n'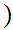 if
m
if
m 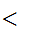 m'
m'
We now
use
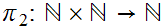 where
where
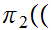 m,n
m,n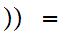 n
to choose the least
n
to choose the least
member
of
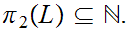 Note that
Note that
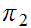 is
one to one on
is
one to one on
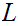 .
.