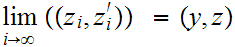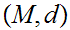 ,
and a subset
,
and a subset
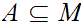 we
say
we
say
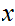 is
a limit point of
is
a limit point of
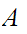 if
if
21.1 Definition:
Given a Metric Space
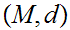 ,
and a subset
,
and a subset
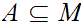 we
say
we
say
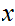 is
a limit point of
is
a limit point of
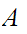 if
if
____________
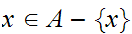 .
.
That is
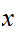 is
in the closure of
is
in the closure of
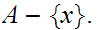
Note:
It is not necessarily the case that the set of limit points of
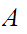 is
the closure of
is
the closure of
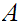 .
.
For
example, a singleton set
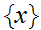 has no limit points but is its own closure.
has no limit points but is its own closure.
21.2 Definition:
A Metric Space,
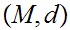 ,
is called compact if every infinite subset
,
is called compact if every infinite subset
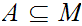 has
a limit point.
has
a limit point.
21.3 Theorem:
The closed unit interval
 0,1
0,1![$\QTR{Large}{]}$](graphics/Compact1__14.png) is compact.
is compact.
Proof:
Choose an infinite subset
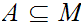 and write
and write
 0,1
0,1![$\QTR{Large}{]=}$](graphics/Compact1__17.png)
 0,
0,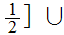
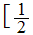 ,1
,1![$\QTR{Large}{]}$](graphics/Compact1__21.png) .
Since
.
Since
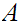 is infinite we can choose one of these subintervals, written
is infinite we can choose one of these subintervals, written
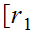 ,
,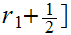 such that
such that
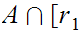 ,
,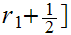 is infinite. Call this intersection
is infinite. Call this intersection
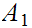 and set
and set
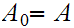
By induction, assume we have chosen a sequence
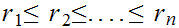 in
in
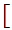 0,1
0,1![$\QTR{Large}{]}$](graphics/Compact1__31.png) ,
and infinite subsets
,
and infinite subsets
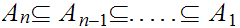
such that
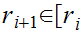 ,
,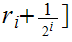
and
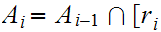 ,
,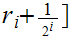
Let
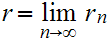 . One verifies that
. One verifies that
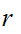 is
in the closure of
is
in the closure of
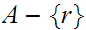 hence a limit point.
hence a limit point.
Assignment: (Due April 20) provide the details.
----------------------------------------------------------------------
Solution:
First note that
 0
0
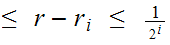
moreover, since
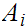 is infinite, we can find
is infinite, we can find
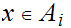 ,
,
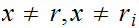 ,
and such that
,
and such that
 0
0
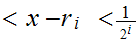
Hence
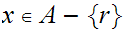 and
and
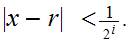
---------------------------------------------------------------------------
21.4 Theorem:
Let
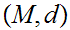 be
a Metric Space. The following are equivalent:
be
a Metric Space. The following are equivalent:
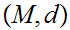 is
compact.
is
compact.
Every sequence in
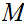 has a convergent subsequence.
has a convergent subsequence.
Proof:
1.
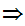 2.
2.
Let
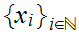 be the sequence. If it only takes on a finite number of different values
select an infinite constant subsequence. If not choose a limit point and a
sequence that converges to that limit point.
be the sequence. If it only takes on a finite number of different values
select an infinite constant subsequence. If not choose a limit point and a
sequence that converges to that limit point.
2.
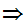 1.
1.
Since
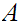 is infinite we can choose a sequence without repeating values. That is a
is infinite we can choose a sequence without repeating values. That is a
map
 such that
such that
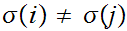 for
for
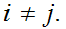 Select a convergent subsequence and a limit point.
Select a convergent subsequence and a limit point.
21.4.1 Corollary:
Every compact Metric Space is complete:
Proof:
A Cauchy sequence is its own "convergent subseqence."
21.5 Theorem:
Given a compact Metric Spaces
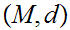 :
:
For any
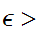 0
and some
n
0
and some
n there exists points
there exists points
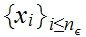
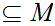
such that
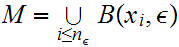 .
.
In particular, M is bounded in the sense that there exists some
b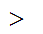 0
such that
0
such that
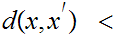 b for
any
b for
any
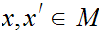 .
.
Proof:
1. Choose any
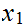 . By induction, suppose we have found
. By induction, suppose we have found
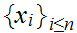 such that
such that
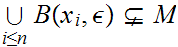 .
Select
.
Select
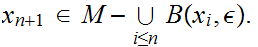 If does not exist then we can find a sequence
If does not exist then we can find a sequence
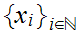 such that
such that
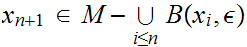 .
However since
.
However since
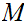 is compact we can find a convergent subsequence
is compact we can find a convergent subsequence
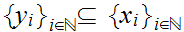 and some
and some
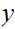
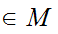 with
with
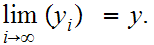 Choose
n such that
Choose
n such that
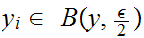 for
for
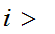 n.
But then for
n.
But then for
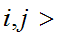 n,
n, 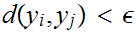 contradicting the choice of
contradicting the choice of
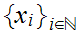 .
.
2.
Choose b
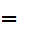 2
2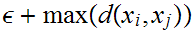 where
where
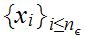 is as in 1.
is as in 1.
Next choose
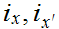 with
with
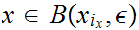 and
and
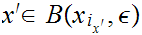 .
.
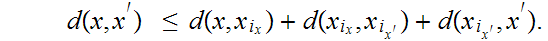
------------------------------------------------------------------------
21.6 Theorem:
Every compact metric space has a countable dense subset.
Proof:
For each
m 0
choose
n
0
choose
n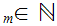 and
and
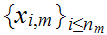
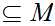
such that
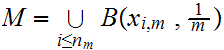 .
.
Clearly
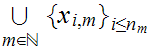 is countable.
is countable.
Assignment: (Due April 20) show that it is dense in
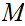 .
.
----------------------------------------------------------------------
Solution:
Select
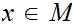 ,
,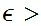 0
0 and
and
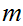 such that
such that
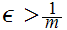
Since
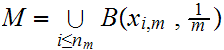
we know that for some i
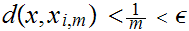
and thus
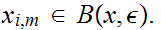
---------------------------------------------------------------------------
21.7 Theorem:
Given Metric Spaces
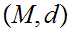 and
and
 with
with
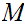 compact, and a continuous map
compact, and a continuous map
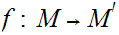 then
then
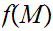 is compact.
is compact.
Proof:
Let
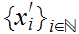
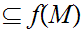 and let
and let
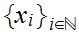 be such that
be such that
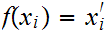 .
Since M is compact we can select a convergent subsequence
.
Since M is compact we can select a convergent subsequence
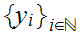 and
and
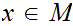 such that
such that
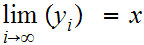 and, by continuity
and, by continuity
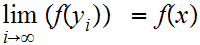 .
But
.
But
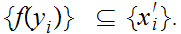
---------------------------------------------------------------------------
21.8 Theorem:
Given Metric Spaces
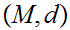 and
and
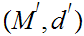 with
with
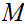 compact, and a continuous map
compact, and a continuous map
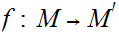 then
then
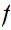 is also uniformly continuous.
is also uniformly continuous.
Proof:
If
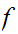 was
not uniformly continuous then there exists some
was
not uniformly continuous then there exists some
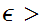 0 such that for any
0 such that for any
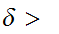 0
there exists
0
there exists
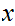 and
and
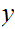 with
with
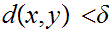 and
and
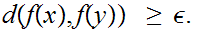
Select sequences
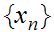 and
and
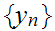 such that
such that
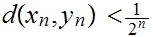 and
and
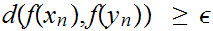
Since M is compact we can assume, without loss of generality that converges.(why?)
let
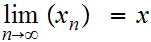 .
.
Since f is continuous we can choose
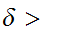 0
such that if
0
such that if
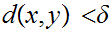 then
then
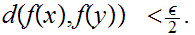
Finally, choose n such that
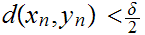 and
and
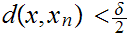
Note that this implies that
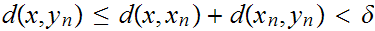
hence
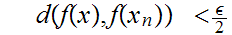
and
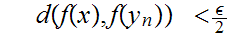
which implies that
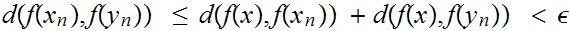
contradicting the definition of the sequences
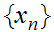 and
and
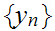 .
.
21.9 Theorem:
Given Metric Spaces
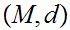 and
and
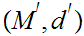 with
with
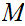 and
and
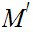 compact,
then
compact,
then
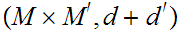 is compact.
is compact.
Proof:
Let
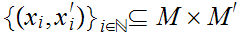 .
Since
.
Since
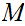 is compact, we can select a subsequence
is compact, we can select a subsequence
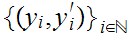 such that the sequence
such that the sequence
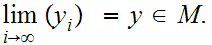
Next, since
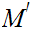 is compact, we can select a subsequence
is compact, we can select a subsequence
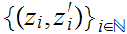 of
of
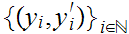 such that the sequence
such that the sequence
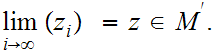
One checks that