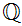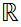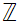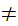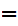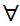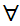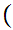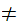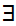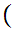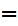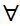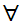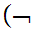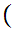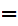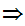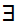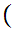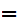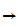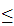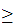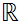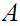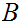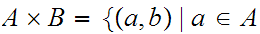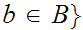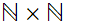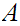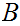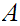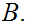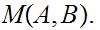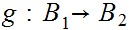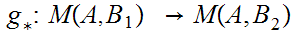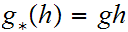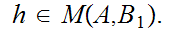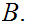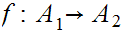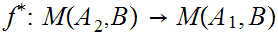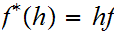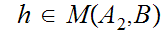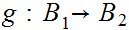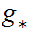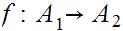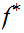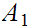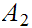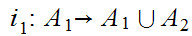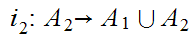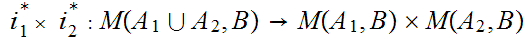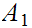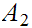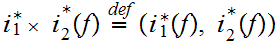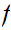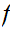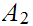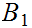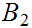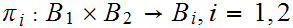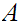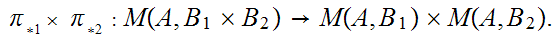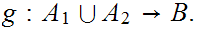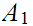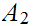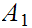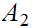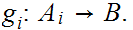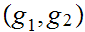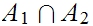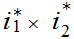0. Background
What
is a Theory?
In Mathematics, a Theory is a
collection axioms and the collection of all statements that can be derived
from them via logical inference.
A theory provides "concrete" model for a "mathematical concept." For example,
Metric Spaces provide a model for sets with a concept of distance between
members of the set.
What is a Theorem?
A Theorem is a statement that can be derived from the axioms
of a Theory.
What was Eilenberg telling us?
Once we know the axioms, the
theorems are determined. Of course, since proofs may be very hard to come by,
finding the theorems for a given theory may be difficult.
In the other hand, the question as to whether a given theory provides a good
model may not have a simple true or false answer. In particular, if a theory
does not provide a good model, the theorems may be true but may not be
particularly interesting or useful.
Indeed, this question, regarding Set Theory will occupy our attention for much
of the Semester
Objects:
Here is a list of familiar objects that will be of interest to us this
semester.
-
 The
Natural numbers {1,2,3,4,.....}
The
Natural numbers {1,2,3,4,.....}
-
 The
Integers {.....,-3,-2,-1,0,1,2,3,4,.....}
The
Integers {.....,-3,-2,-1,0,1,2,3,4,.....}
-
 The
Rational numbers
The
Rational numbers
{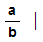 a
a 0,
b
0,
b 1
or pairs a,b with
a
1
or pairs a,b with
a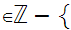 0
0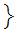 b
b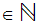 and
gcd(
and
gcd( a
a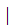 ,b)
,b)
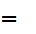 1)}
1)}
The reason for all this formality is to be sure that there is
a unique representation of each rational.
-
 The
Real numbers
The
Real numbers
-
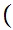 0,1
0,1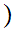 All
Real numbers x such that
0
All
Real numbers x such that
0 x
x 1.
More formally, {x
1.
More formally, {x
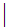 x
x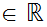 and
0
and
0 x
x 1}
1}
-
 The
Complex numbers
The
Complex numbers
-
Many Others
Language:
First some logical notation:
-
The symbol
 is
to be read "there exists."
is
to be read "there exists."
-
The symbol
 is
to be read "for every."
is
to be read "for every."
-
The symbol
 is
to be read "not"
is
to be read "not"
-
The symbol
 is
to be read "implies"
is
to be read "implies"
The context that this notation will appear will be in the "language of Sets."
In particular, whether or not a given property holds will depend on the Set
that it belongs to.
Here are two examples, the second of which we will write in the more informal
notation that we will use almost everywhere in these notes :
-
The first example, in increasingly formal language, is a
statement that is true
for 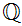 and
and
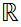 ,
but not for
,
but not for
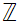 .
Try to
solve 3z
.
Try to
solve 3z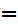 2.
2.
-
Let f:[0,1]
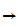 [0,1]
be a continuous function then there exists an x such that
f(x)=x. You might remember the proof is just the
intermediate value theorem, using g(x)=x-f(x). One
notes that
g(0)
[0,1]
be a continuous function then there exists an x such that
f(x)=x. You might remember the proof is just the
intermediate value theorem, using g(x)=x-f(x). One
notes that
g(0)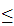 0
and
g(1)
0
and
g(1)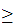 0.The
statement is not true if you replace [0,1] by
0.The
statement is not true if you replace [0,1] by
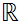 .
Just choose f(x)=x+1.
.
Just choose f(x)=x+1.
![$\vspace{1pt}$]()
![$\vspace{1pt}$]() The
Algebra of Sets
The
Algebra of Sets
Sections 1.1, 1.2, 1.4, and 1.5 cover what should be fairly familar territory
in elementary set theory, unions, intersections, functions, equivalence
relations, etc. (Assignment: Read this material and bring any
questions to the next class)
We will want to look at products of sets. That is if
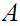 and
and
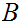 are sets
are sets
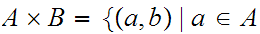 and
and
eg:
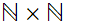 The
set of ordered pairs of Natural Numbers.
The
set of ordered pairs of Natural Numbers.
If
 and
and
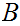 are sets, we will want to look a sets of functions (we will often use the term
"map") from
are sets, we will want to look a sets of functions (we will often use the term
"map") from
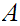 to
to
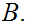 We use the notation
We use the notation
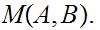
There is some important algebra here as well.
0.1 Definitions:
a. Fix
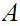 .
Suppose we are give a map
.
Suppose we are give a map
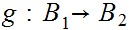 . We define a map
. We define a map
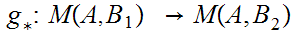 by the formula
by the formula
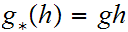 for
for
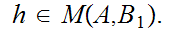
b. Now fix
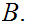 Suppose
we are give a map
Suppose
we are give a map
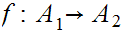 . We define a map
. We define a map
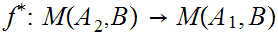 by the formula
by the formula
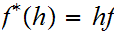 for
for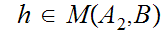 .
.
0.2
Lemma;
In the setting of 0.1
a. Suppose
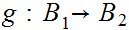 is one to one then
is one to one then
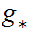 is one to one.
is one to one.
b. Suppose
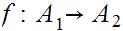 is onto then
is onto then
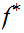 is one to one.
is one to one.
Proof: Exercise(hint: immediate from the definitions)
0.3 Lemma:
a. Let
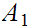 and
and
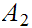 be sets. Let
be sets. Let
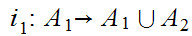 and
and
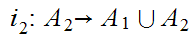 be
the inclusions. Then, for any set
be
the inclusions. Then, for any set
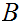 ,
the map
,
the map
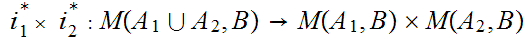
is 1 to 1. If
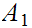 and
and
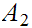 are disjoint then it is also onto.
are disjoint then it is also onto.
Note:
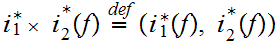 ,
the ordered pair of maps
,
the ordered pair of maps
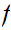 restricted
to
restricted
to
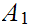 and
and
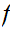 restricted
to
restricted
to
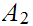 .
.
b. Let
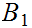 and
and
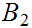 be sets. Let
be sets. Let
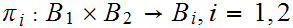 be the projection onto the "ith" axis. For any set
be the projection onto the "ith" axis. For any set
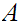 ,
the map
,
the map
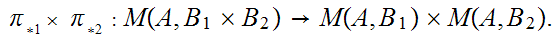
is a 1 to 1 and onto.
Proof:
a.
Cutting through the notation, the proof is little more than observing
that any map
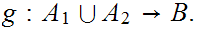 Is
uniquely determined by its values on
Is
uniquely determined by its values on
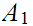 and
and 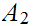 .
.
If
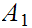 and
and
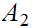 are disjoint then any pair of maps
are disjoint then any pair of maps
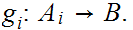 can be combined to give a map on
can be combined to give a map on
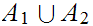 . If not, only pairs
. If not, only pairs
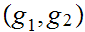 agreeing on
agreeing on
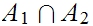 can be so combined, hence
can be so combined, hence
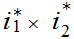 is only 1 to 1.
is only 1 to 1.
b. is even more straight forward.
 The
Natural numbers {1,2,3,4,.....}
The
Natural numbers {1,2,3,4,.....}
 The
Integers {.....,-3,-2,-1,0,1,2,3,4,.....}
The
Integers {.....,-3,-2,-1,0,1,2,3,4,.....}
 The
Rational numbers
The
Rational numbers
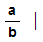 a
a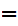 0,
b
0,
b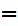 1
or pairs a,b with
a
1
or pairs a,b with
a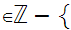 0
0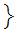 b
b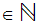 and
gcd(
and
gcd(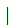 a
a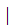 ,b)
,b)
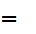 1)}
1)}
 The
Real numbers
The
Real numbers
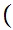 0,1
0,1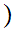 All
Real numbers x such that
0
All
Real numbers x such that
0 x
x 1.
More formally, {x
1.
More formally, {x
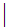 x
x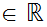 and
0
and
0 x
x 1}
1}
 The
Complex numbers
The
Complex numbers