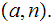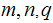 be three integers . We write
be three integers . We write
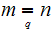 if
if
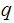 divides
divides
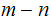 .
.
A Bit More Number Theory
Notation: Let
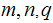 be three integers . We write
be three integers . We write
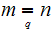 if
if
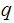 divides
divides
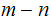 .
.
Note that from the previous section we have
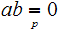 implies
implies
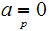 or
or
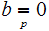
Lemma:
Let
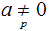 ,
,
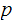 prime, then there exists an
integer
prime, then there exists an
integer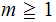 such that
such that
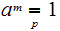
 PROOF:
A simple counting argument shows that there are integers
PROOF:
A simple counting argument shows that there are integers
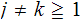 with
with
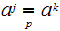 .
.
Assume
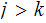 .
We have
.
We have
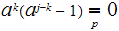 .
But since
.
But since
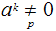 we have
we have
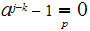 .
.
Lemma: Let
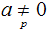 then
then
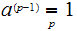 .
.
PROOF: Let
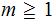 be the least integer such that
be the least integer such that
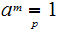 .
It suffices to show that
.
It suffices to show that
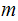 divides
divides
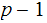 .
To do this consider the set of integers.
.
To do this consider the set of integers.
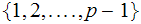 ,
We can divide this set into disjoint subsets of
,
We can divide this set into disjoint subsets of
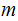 elements using the relationship
elements using the relationship
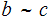 iff
iff
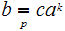 for some
for some
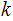 .
.
Observations: The subsets are of the form
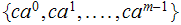 .
The other points is that
.
The other points is that
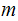 depends on the
depends on the
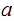 .
For example, let
.
For example, let
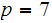 and
and
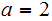 .
Note
.
Note
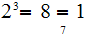 .
On the other hand, if
.
On the other hand, if
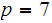 and
and
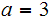 , we have
, we have
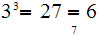 Of course,
Of course,
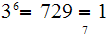 .
.
Theorem: Let
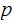 and
and
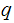 be primes. Let
be primes. Let
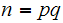 .
Let
.
Let
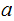 be relatively prime to both
be relatively prime to both
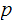 and
and
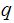 , hence
, hence
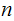 ,
then
,
then
 .
.
Hence,
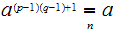 .
.
PROOF: Both
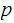 and
and
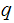 , divide
, divide
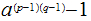 .
(
.
(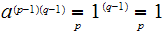 )
)
Observation: Another way of looking at this is
that
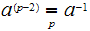 and
and
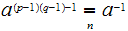 Of course, the Extended Euclidean Algorithm tells us that
Of course, the Extended Euclidean Algorithm tells us that
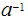 can
be computed for any relatively prime pair
can
be computed for any relatively prime pair