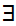 x
x
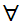 y
(Shave(x,y)
y
(Shave(x,y)
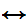
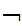 Shave(y,y))
Shave(y,y))
"One of themselves, even a prophet of their own, said, the Cretians are alway liars, evil beasts, slow bellies. This testimony is true."
Titus 1:12-14 (King James Version)
Definition:
A paradox is a statement or group of statements that lead to a logical self-contradiction. For example,
The next bulleted statement is a lie.
The previous bulleted statement is true.
Proposition:
There is a barber who lives on an island. The barber shaves all those men who live on the island who do not shave themselves, and only those men.
Question:
Does the barber shave himself?
Answer:
If the barber shaves himself then he is a man on the island who shaves himself hence he, the barber, does not shave himself. If the barber does not shave himself then he is a man on the island who does not shave himself hence he, the barber, shaves him(self).
Analysis:
This is not actually a paradox.
Consider the proposition Shave(x,y) which is true if x shaves y and false if x does not shave y. We can restate the proposition as:
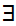 x
x
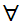 y
(Shave(x,y)
y
(Shave(x,y)
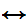
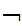 Shave(y,y))
Shave(y,y))
There exists an x such that for every y, x shaves y iff y does not shave y.
Suppose this proposition were true. Let b be the x whose existance is hypothesized. thus
 y
(Shave(b,y)
y
(Shave(b,y)
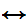
 Shave(y,y))
Shave(y,y))
Since this holds for all y it holds for
y b.
So
b.
So
Shave(b,b)
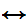
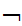 Shave(b,b)
Shave(b,b)
Hence one may hypothesize that the proposition is false. It is worth checking that this hypothesis does not also lead to a contradiction.
Suppose
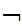 (
(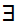 x
x
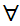 y
(Shave(x,y)
y
(Shave(x,y)
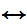
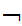 Shave(y,y)))
Shave(y,y)))
Or
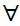 x(
x(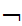 (
(
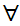 y
(Shave(x,y)
y
(Shave(x,y)
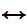
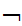 Shave(y,y)))
Shave(y,y)))
Or
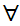 x
x
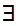 y
y
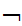 (Shave(x,y)
(Shave(x,y)
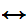
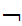 Shave(y,y))
Shave(y,y))
Which is no problem since if for any x if we chose
y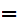 x
it is certainly the case that
x
it is certainly the case that
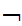 (Shave(x,x)
(Shave(x,x)
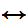
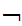 Shave(x,x))
Shave(x,x))
For any meaning of Shave(x,x)!!!!!!
Of course there is no problem if the barber ferries in from the mainland. In particular, he is not a member of the "set" of people on the island referred to in the second sentence of the proposition.