
The Seven Bridges of Konigsberg Over the River Pregel:

Is there a route over the seven bridges that only traverses each bridge once?
Method 1:
Label the bridges
 and
and
 .
Try the
.
Try the
 possibilities.
possibilities.
Method 2:
Consider the associated Graph:

and argue about traversal properties of nodes with an odd/even number of edges. In particular, in a "one-time traverse"
of a node with a even number of edges - a path both begins and ends there, or neither begins nor ends there .
of a node with a odd number of edges - a path must begin there or end there but not both.
Theorem:
There does not exist a rational number
 such that
such that

PROOF:.
Fundamental Lemma of Number
Theory: Let
 be two integers. There exits unique integers
be two integers. There exits unique integers
 and
and
 with
with
 and
and

Note: Uniqueness follows from the
fact that
 implies
implies

Definition: Let
 be two integers. The greatest common divisor of
be two integers. The greatest common divisor of
 and
and
 is defined to be largest integer
is defined to be largest integer
 such that
such that
 divides both
divides both
 and
and
 .
(
.
( ).
).
Since
 divides both
divides both
 and
and
 , we can use induction to show that
, we can use induction to show that
 exists. For that matter, since
exists. For that matter, since
 one can compute
one can compute
 (very inefficiently!) by
(very inefficiently!) by
trying all values, starting at
 and ending at the least of
and ending at the least of
 and
and

Examples:
 .
.


Lemma: Suppose
 then
then
 .
.
 PROOF:
In fact all of their common divisors are in common!
PROOF:
In fact all of their common divisors are in common!
The Euclidean Algorithm for
computing  :
:
Theorem( Extended Euclidean Algorithm): Let
 There exists integers
There exists integers
 and
and
 , computable using the Euclidean Algorithm such that
, computable using the Euclidean Algorithm such that

 PROOF:
(By induction)
PROOF:
(By induction)
If
 the theorem is trivial so for simplicity assume that
the theorem is trivial so for simplicity assume that
 .
Again if
.
Again if
 divides
divides
 the theorem is trivial so assume
the theorem is trivial so assume

 hence
hence
If
 divides
divides
 then
then
 and
and
 .
.
Otherwise

 hence
hence and
and
 or
or
 again if
again if
 divides
divides
 we are done else......
we are done else......
Example- Compute

Computing the simple-minded way requires
 long divisions. Divide
long divisions. Divide
 and
and
 by
by
 through
through
 .
.
Now by the euclidean algorithm,





This admittedly is an easy example but we see that EA requires
 long divisions to find
long divisions to find
 .
.
Lemma: Suppose
 is prime (the only divisors are
is prime (the only divisors are
 and
and
 ).
Suppose
).
Suppose
 divides
divides
 then
then
 divides
divides
 or
or
 divides
divides
 .
.
 PROOF: Suppose
PROOF: Suppose
 does not divide
does not divide
 ,
then
,
then
 .
Thus there exists integers
.
Thus there exists integers
 and
and
 , such that
, such that

Multiplying both sides of the equation by
 gives
gives

Finally, setting
 we get an explicit divisor
we get an explicit divisor

In particular,

Proof that
there does not exist a rational number
 such
that
such
that

Let
 .
Assume
.
Assume
 Given
a pair
Given
a pair
 we
know how to calculate
we
know how to calculate
 !
Multiplying, we have
!
Multiplying, we have
 .
Since
.
Since
 divides
divides
 we conclude from the lemma above (again a
calculation) that
we conclude from the lemma above (again a
calculation) that
 for some
for some

Hence
 or
or
 .
Hence as before
.
Hence as before
 .
Thus
.
Thus
 .
.
Theorem: Let f:[0,1]
 [0,1]
be a continuous function then there exists an x such that f(x)
= x.
[0,1]
be a continuous function then there exists an x such that f(x)
= x.
This is a consequence of the following
Intermediate Value Theorem: Let f:[0,1]

 be
a continuous function. Let
f(0)
be
a continuous function. Let
f(0) c
c f(1).
Then there exists
a
f(1).
Then there exists
a [0,1]
such that f(a)
[0,1]
such that f(a)
 c.
c.
To see how the first result follows from the second apply the intermediate
value theorem to g(x)=x-f(x).
One notes
that g(0) 0
and g(1)
0
and g(1) 0
0
We will discuss this result in some detail, and in greater generality, in the second part of this course. The following brief discussion is simply meant to remind about the nature of the Real numbers and to continue to set the stage for our discussion of Set Theory. We begin with Dedekind's definition of the real numbers.
Definition: A Dedekind cut of the Rationals,
 , is a subset
, is a subset


 that satisfies these properties:
that satisfies these properties:
1.
 is not empty.
is not empty.
2.
 is not empty.
is not empty.
3.
 contains no greatest element
contains no greatest element
4. For
 if
if
 and
and
 ,
then
,
then
 .
.
 the set of "Real Numbers" is defined to be the set of all Dedekind cuts of
the set of "Real Numbers" is defined to be the set of all Dedekind cuts of
 Note that in the definition only the "order property" of
Note that in the definition only the "order property" of
 is used. We could, in fact, generalize the definition of Dedekind cuts by
simply replacing
is used. We could, in fact, generalize the definition of Dedekind cuts by
simply replacing
 with an appropriatley ordered set. One would then write something like
with an appropriatley ordered set. One would then write something like
 .
.
Examples:
Let
 be a rational. Let
be a rational. Let
 all
all
 . We can consider
. We can consider


 by observing that different rationals generate different Dedekind
cuts.(Exercise: Why?)
by observing that different rationals generate different Dedekind
cuts.(Exercise: Why?)
 . Let
. Let
 all
rationals
all
rationals
 all positive rationals
all positive rationals
 such that
such that
 .
This gives us a "construction" of
.
This gives us a "construction" of

Let
 be a strictly increasing sequence of rational numbers that is bounded
above.
be a strictly increasing sequence of rational numbers that is bounded
above.
Define
 all
all
 such that there exists an
such that there exists an
 with
with
 .
.
All bounded increasing sequences in
 have limits in
have limits in
 (WHY?)
Note:
(WHY?)
Note:
 is
correct, since by assumption
is
correct, since by assumption
 we know
we know

More generally, Let
 .
Be an arbitrary set of Dedekind cuts that is bounded above, then
.
Be an arbitrary set of Dedekind cuts that is bounded above, then
 is a Dedekind cut. Bounded above simply means that there is some
is a Dedekind cut. Bounded above simply means that there is some
 such that
such that
 for any
for any
 .
.
Let
 be
a finite set of Dedekind cuts, then
be
a finite set of Dedekind cuts, then
 is a Dedekind cut.
is a Dedekind cut.
Exercise:(to be turned in Wednesday Jan 26) Prove 4. and 5.
Solution for 4.:
We need check the the 4 properties of a Dedekind cut hold.
1. Since
 ,
,

2. Since
 for any
for any
 ,
,
 , hence
, hence

3. Let
 then
then
 for
some
for
some
 ,
since
,
since
 is
a cut there is some
is
a cut there is some
 with
with
 .
.
But
 implies
implies
 .
.
4. Is essentially the same argument.
Solution for 5.:
1. Choose
 and let
and let
 since we only have a finite number of
since we only have a finite number of
 this
makes sense. Since
this
makes sense. Since
 and
and
 for
all i.
for
all i.
 for
all i. Hence
for
all i. Hence
 .
.
2. Since

 and
and

 we
can conclude that
we
can conclude that

 .
.
3. Let
 , choose
, choose
 with
with
 .
Now let
.
Now let
 As
in 1. this exists. Check that
As
in 1. this exists. Check that
 for all i, hence
for all i, hence
 and
and
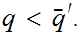
4. Is immediate since if
 ,
and
,
and
 ,
then
,
then
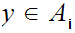 for all i. hence
for all i. hence
 .
.
Exercise:(to be turned Wednesday Jan 26). Consider the set of positive infinite decimal fractions

 where
where
 0,1,2,3,4,5,6,7,8,9
0,1,2,3,4,5,6,7,8,9 and there does not exist an n such that
and there does not exist an n such that
 0
for
n
0
for
n i
i
Show that there is a 1 to 1 order preserving map from set of positive infinite decimal fractions to the appropriate set of Real numbers.
Solution :
Let
 to be more precise
to be more precise

Since the infinite decimal fractions is bounded above by 1,
we can apply 4. above to conclude
 is a cut.
is a cut.
To see that distinct fractions result in distinct cuts, we begin by noting
that
 and since the infinite decimal fraction does not end in a string of
0s, there is some m with
and since the infinite decimal fraction does not end in a string of
0s, there is some m with

Assume



 . Specifically, there is an n with
. Specifically, there is an n with



 . One checks that this implies that for all n,
. One checks that this implies that for all n,
 ,
hence
,
hence

 . On the other hand since we can choose some s with
. On the other hand since we can choose some s with
 we have
we have
 . Thus
. Thus

Observation :
Based on the examples above and the fact that there does not exist a rational
number
 such that
such that
 we have
we have


 .
.
Definitions:
Real numbers can be compared. Let
 and
and
 be real numbers we define
be real numbers we define


 if
if

 .
One can also extend the rules of arithmetic so as to give the expected
properties of the Real numbers.
.
One can also extend the rules of arithmetic so as to give the expected
properties of the Real numbers.
Comments:
After making the appropriate observations one might ask if the Dedekind
process could be repeated? In particular,
 , itself, is a candidate for extension by Dedekind cuts. But,in fact, one can
show that the inclusion
, itself, is a candidate for extension by Dedekind cuts. But,in fact, one can
show that the inclusion


 (
( )
is 1 to 1 and onto.
)
is 1 to 1 and onto.
Thus, for example, one can revise Example
3. to show that all bounded increasing sequences in
 have limits in
have limits in
 .
This is the heart of the Intermediate Value Theorem
.
This is the heart of the Intermediate Value Theorem