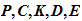 )
where the following conditions are satisfied:
)
where the following conditions are satisfied:
Definition 1.1: A cryptosystem is a
five-tuple
(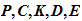 )
where the following conditions are satisfied:
)
where the following conditions are satisfied:
1.
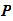 is a finite set of possible plaintexts:
is a finite set of possible plaintexts:
2.
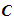 is a finite set of possible ciphertexts:
is a finite set of possible ciphertexts:
3.
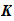 the keyspace, is the a finite set of possible
keys:
the keyspace, is the a finite set of possible
keys:
4. For each
K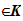 there is and encryption rule e
there is and encryption rule e
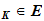 and a corresponding decryption rule
d
and a corresponding decryption rule
d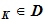 .
Where
.
Where
e
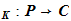 and d
and d
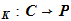 are functions such that for all
are functions such that for all
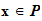 ,d
,d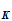 (e
(e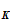 (
(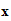 ))
))
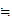
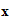 .
.
For the purposes of these examples, we use a-z and 0-25 interchangeably.
1. The Shift Cipher :
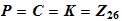 and
and
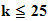 ,
,
e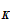 (
(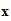 ))
))
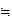
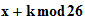
and
d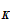 (
(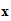 ))
))
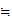
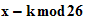
Observations (not as trivial as they seem) :
1. If I
knew it was that a message was coded with a shift cipher and I knew one
example (e.g.
e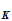 (
(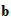 )
)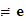 )
then I
)
then I
could
decode any message. (e.g.
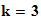 )
)
2. If I knew the rule
e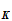 (
(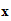 ))
))
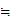
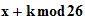
I could deduce the rule
d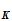 (
(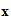 ))
))
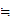
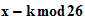
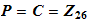 and
and
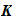 is the set of all possible permutations,
is the set of all possible permutations,
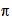 ,of
the alphabet ,
,of
the alphabet ,
For example (a typewriter cipher)
e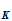 (
(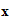 ))
is computed from the following table
))
is computed from the following table
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| m | l | p | n | k | o | b | j | i | v | h | u | c | g | y | x | f | t | z | d | r | s | e | a | w | q |
Observations :
1. If I knew it was that a message was coded with a substitution cipher and I knew 25 of the substitutions then I
could deduce the 26th and decode any message. Can I do better? (To be continued in our discussion
of Information Theory)
2. If I knew the rule
e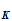 (
(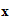 ))
))
I could deduce the rule
d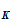 (
(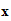 ))
))
with a bit of work.
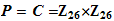 and
and
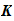 is the set of all possible permutations,
is the set of all possible permutations,
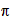 ,of
pairs of letters of the alphabet ,
,of
pairs of letters of the alphabet ,
e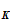 (
(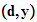 ))
))
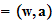 - Break the message up into pairs of letters and map each pair. (maybe you
have to pad the message string with an
- Break the message up into pairs of letters and map each pair. (maybe you
have to pad the message string with an
addition letter.
Observations :
1. I would have to know a lot more then in 2. above.
2. If I knew the rule
e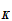 (
(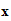 ))
))
I could deduce the rule
d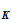 (
(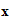 ))
))
with a lot of work. A computer would help.
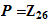 ,
,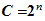 for some
for some
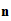 , and
, and
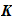 is the set of injective maps (1 to 1) of the alphabet to
is the set of injective maps (1 to 1) of the alphabet to
the set of binary sequences of length
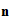 .
.
Observations :
1. ASCII is a Binary Cipher of length 8.
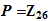 ,
,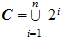 for some
for some
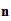 , and
, and
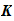 is the set of injective maps (1 to 1) of the alphabet to
is the set of injective maps (1 to 1) of the alphabet to
the set of binary sequences of length
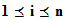 .
.
Observations :
1. Morse code is a binary cipher of length less than or equal to 6.
The International morse code characters are:
|
|
|
|
2. Latter we will consider compression algorithms that create variable length cyphers. When we discuss Information Theory we will we will show the existance of "best possible" codes from the point of view of transmission times.