
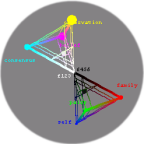
An interesting visualization for a set of four probabilities (or other positive numbers which sum to 1) involves a tetrahedron (3-simplex). The example below is labeled to document the fractional allocation of an individual's attention across niche levels on the four layers of organization which constitute the lion's share of attention in many mammal communities. Move your mouse over the model and it should start rotating. The grey dot and internal plane contours shown here denote the equal-probability assignment {1/4,1/4,1/4,1/4}. Although you can already spin and zoom in on this model, we are planning to post a version with adjustable probabilities and labels for use with your own applications here in the days ahead...
Below are a variety of fractional-attention assignments for illustration, and some possible associations therewith. At present these are images but not models, so they won't rotate. The top two ({1/3,1/3,1/3,0} and {.1,.1,.1,.7}) refer to the allusion by Jared Diamond, for example, that large animals which give little regard to hierarchy in their natural communities have been quite resistant to domestication. The "party animal" assignment (sans negative connotation) in the lower left corner, namely {1/2,1/2,0,0}, simply refers to an organism invested in friendships and self, without regard to elements of the larger picture. Others have pointed out, for example, that it might also characterize youngsters of a species who've not yet shouldered the responsibilities of an adult. In fact, observations by Piaget and others about stages of learning in children might suggest a pattern of emergent awareness along organization scales focussed inward, then outward, in sequence from metazoan skin, gene-pool, and idea-pool boundaries, i.e. an element of function rather than structure where ontogeny mimics phylogeny. What do you think?

Using the same fractional-attention model to illustrate, we might also visualize (below) a distribution of 100 individuals (small dots) randomly distributed over six niche-layer probabilities f1 through f6 which add up to 1. Here these are graphed using f1+f2+f3 at the dark vertex, f4 at the red vertex, f5 at green, and f6 at blue. The center point at {1/2,1/6,1/6,1/6) is marked with a larger dot, as well as the internal plane markings introduced above. One might technically define outlying individuals (like the one near the red-yellow-green edge) as extremist by virtue of their activity focus, independent of the sides they do or don't take on any given issue. In this sense, one lessens extremism by increasing the multiplicity of scales through which individuals are connected to the world around. Dynamical modeling of such probabilities might of course examine the flow of such dot clusters in the face of external developments over time.
Rather than divide the six probabilities according to the locality of their focus as above (i.e. f123 on one end and f456 on the other), one might instead divide them according to the direction of focus with respect to their associated physical boundary (i.e. f135 on one end and f246 on the other). This might be useful for highlighting differences between individuals along the continuum between "nurture" and "explore", e.g. to examine the nature or absence of correlations with gender. These are only two examples of the way that strategically chosen simplex representations can make patterns, hidden within a collection of six probabilities, accessible to the limited perceptions of us denizens of (3+1)D spacetime.