Metric-based approaches to mechanics allow one to accomplish a great deal in context of a single reference frame of yardsticks and synchronized clocks, before moving to considerations that involve more than one such frame. One of these things is the quantitative treatment of accelerated motion. This is especially clear if one plots velocity-parameters derived from the metric equation e.g. coordinate-velocity v=dx/dt, proper-velocity w=dx/dτ, and gamma γ=dt/dτ as a function of map-position. Rather complex scenarios, like that of an accelerated-twin adventure, can be illustrated in very quantitative and concrete terms. Such plots can be made dimensionless in terms of a fixed constant proper-acceleration α. Since these apply locally to all accelerated motions (even in curved spacetime), we refer to them here as "universal acceleration plots".
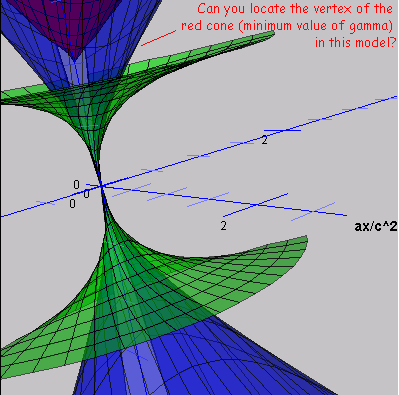
In this context, below find an interactive plot of velocities (green is coordinate-velocity or v=dx/dt; blue is proper-velocity or w=dx/dτ) and gamma (red is speed-of-map-time or γ=dt/dτ=E/mc2) for a system undergoing constant proper-acceleration α, versus displacement parallel and perpendicular to that acceleration. All distances (and simultaneity) are defined with respect to a single reference "map-frame". The velocity-axis is in the "facing funnel" direction, while perpendicular displacements lie along the "butterfly symmetry axis". The section of the universal plot provided here covers values of coordinate-velocity v (green) for map-times t between -2 and 2, and of proper-velocity w (blue) for proper-times τ between -2 and 2, with all times measured relative to the "turn-around" event (vx=0) in units of c/α (or years at 1 gee). Values of transverse coordinate-velocity (a constant for a given trajectory) range from -0.9c to 0.9c (i.e. around 2 lightyears/traveler year). The red surface represents γ for x-distance traveled relative to rest of 0 to +2, in units of c2/α (or lightyears at 1 gee).
Here comes the applet...
Universal acceleration plots are useful, for example, if one wants to visualize an accelerated-twin adventure in concrete terms. A (1+1)-dimensional example of this is shown below. Please excuse the arcane "one-map three-clock" nomenclature, which in addition to the above velocities plots map-time t and proper-time τ in dimensionless form, as well as "chase-plane" time T and "Galilean-kinematic" velocity V=dx/dT, for which the chase-plane trajectory has been chosen so that Galileo's constant acceleration equations describe the motion of our accelerated traveler. The most interesting times and velocities, of course, are the ones mentioned above: map-time t and coordinate-velocity v=dx/dt, as well as the less frame-variant quantitites: proper-time τ, proper-velocity w=dx/dτ, and gamma γ=dt/dτ.


Note in the changing plot on the right that as the round trip duration and maximum velocity decreases, the time-lapse disagreements between traveler and map get smaller. As the trip becomes longer, traveler time elapsed can become almost negligible in comparison to map time.
Related links: Some constant acceleration calculators in
java and
javascript.
Even newer, a Live3D
platform
for empirical studies of spacetime.
For more on the variables here, see this slide,
this PDF,
or  .
Related notes:
anyspeed modeling,
metric-smart
mechanics,
and
one-map two-clocks.
You might also enjoy some of our
nanoexploration
and information
physics tools.
.
Related notes:
anyspeed modeling,
metric-smart
mechanics,
and
one-map two-clocks.
You might also enjoy some of our
nanoexploration
and information
physics tools.
This site hosted by the UM-StL Dept. of Physics and Astronomy 2005 © P. Fraundorf. Mindquilts site page requests ~2000/day approaching a million per year. Requests for a "stat-counter linked subset of pages" since 4/7/2005: .
