


[outer row fixed] [board games] [one parameter + spiral] [t-shirt topology] [links]
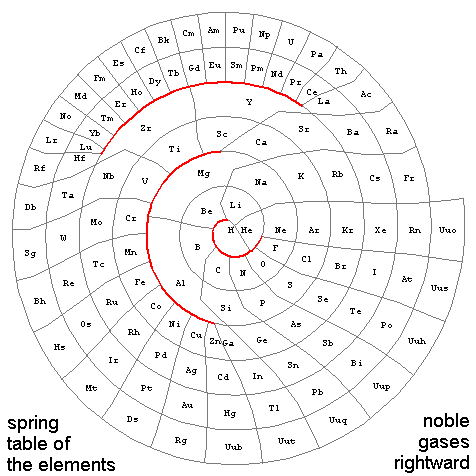
These maps treat elements as movable beads-on-a-track, connected with springs if they are adjacent in atomic number and/or in outer electronic shell similarity. The first example below holds hydrogen and the noble gases fixed, as well as the elements heavier than xenon, while letting all the other elements slide along the track under the influence of equal strength springs. Calculation of the resulting elemental positions with Mathematica yields something like...

If you further allow elements in the next to last row of the track (out to radon) to slide, in hopes of making connections in the map above somewhat less zig-zag, the rare earths run into the transition metals unless one weakens the springs e.g. beyond argon. However, if you let all elements except hydrogen and the noble gases relax their positions, the "identical-spring" strategy continues to work. The resulting pattern, with the position of all elements determined by letting them choose, yields an aesthetically pleasing connectivity map:

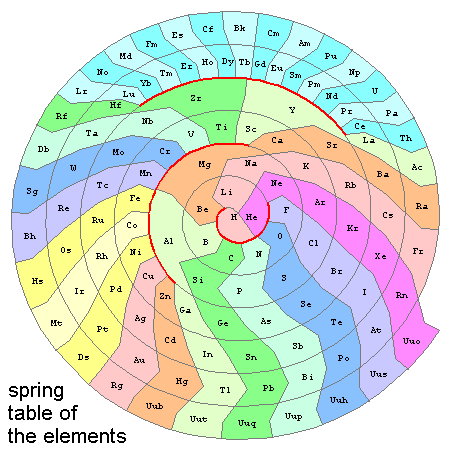
The color scheme above has group 0 (noble gases) magenta, group 1 (electro-positive alkali metals) red, group 2 (alkali earths) brown, group 3 (boron group) dark green, group 4 (carbon group) bright green, group 5 (nitrogen group) blue green, group 6 (chalcogens) dark blue, group 7 (electro-negative halogens) bright blue, group 8 (including some noble metals) yellow, and rare earths cyan. Since some of the elements at the edge of transition regions get pushed a bit closer together, the labeled map below is given a bit more space.

Does this plot illustrate any relationships you had not been aware of before. For example, does it tell you why nanotubes can be made from both carbon and boron nitride, why water soluble salts include alkali halides, why GaAs and InSb and CdTe may have both structures and semiconducting properties like those of Si and Ge, or why the actinide rare earths (including uranium) are geologically associated with phosphates and hence abundant in most hand soaps? Why do the plot bifurcations between H:He (filled with Be through F), Mg:Al (filled with Sc through Zn), and Y:Zr (filled with the rare earths) mean something different in each case about their relationships to the next-row elements in the openings that result? More discussion of these relationships may be found here.
Ideas for recoloring to better illustrate property similarities, and/or for turning this plot into an area map for a board game (e.g. as you traverse the spiral and cross the alkali metals branch, hope that you don't draw the rain card), are invited. In the meantime, what will happen if one tries to relax the positions of all elements except hydrogen, or perhaps hydrogen and the noble gas ununoctium 118Uuo? Then what happens if you remove the track?
Postscript (8/09/2005): On the subject of board games and curvy tables, check out this sketch with the three "no-crossing lines" highlighted in red. These bifurcations show up clearly as self-similar loops in Melinda Green's periodic fractal. The spring-designed plot here is more symmetric and less interesting, but otherwise topologically equivalent to Green's fully-connected version of the familiar periodic table. Who knows, upon further relaxation of positions (see discussion above about allowing the atoms even more freedom to "go where they want") those red gaps might open up, with this plot starting to look even more like the other.
You might also enjoy comparing this to some other periodic table styles. To that end the panel below (from Chris Heilman's collection) has been adapted (by adding Green's & this layout to the right) and posted here with permission.

Second Postscript (8/10/2005): Allowing all elements except hydrogen and helium to go where they want on the wire yields a slightly wilder layout. It looks a bit like someone's hair is on fire, or a female wolf spider with glow-in-the-dark appendages and blue-green babies on its back.


This map has only one free parameter: the ratio (here ~2.5) between the rest-length of all springs and the H-He distance. Basically, this determines (or is determined by) the angle subtended at He between H and Li. Everything else is decided by the balance of forces between connected elements. Labeled, we get...

The table form, rotated to match the modern periodic table with noble gases on the right, is shown below. Given positions for hydrogen, helium (specifying scale and orientation) and lithium (specifying spring constant), all the other elements have literally decided where to go on their own. The patches for each element were then defined with a simple algorithm for locating intermediate vertices on spiral paths of the wire, and its 180 degree complement (which serves here to define the one continuous periodic table "row"). As you might expect, this table has fifty elements in eight long (6 or 7 entry) "main-element" columns on the lower right, forty elements in ten intermediate (4-entry) "transition-metal" columns, and twenty-eight elements in fourteen short (2-entry) "rare-earth" columns at the top.
One goal of the board game might be to start at hydrogen, and then move your "piece" in turns onto each of the other elements (or e.g. only that subset with stable isotopes) via adjacent hops, authorized by correctly answering a randomly-drawn question about the relationship between elements on opposite sides of the proposed hop. Any volunteers to help put together a web-version of this game?
Third Postscript (8/13/2005): Removing the wire clearly transforms the problem to one of a local minimum in elastic energy, rather a global one. We're working on finding a path to that local minimum without collapse of the structure into a tangle, but we're not there yet. Stay tuned.../pf
Fourth Postscript (2/11/2006): Although we are still not sure about 2D spring arrangements, in three dimensions a spring-connected periodic table relaxes nicely. And guess what: It has the topology of a t-shirt! Here are some interactive versions of that 3D net which might be fun to play and/or teach with. The t-shirt topology in turn suggests a way to display all of these elemental connections in tabular (nearly rectilinear) form, as shown below (Technical Drawing Copyright 3/1/2006 VAu697-466). There a black line charts the path of the atomic-number spiral, while columns of elements all flow from one of three red-bordered (bifurcation) openings. The main element groups pour in from the top (the T-shirt's left sleeve), transition metal groups from the central opening (the T-shirt's collar), and rare earth groups from the bottom (the T-shirt's right sleeve). The animation to the right shows how the Z-spiral (black) on such a T-shirt would wrap around in three dimensions, yielding a periodic table with a single continuous row, and one bifurcation point (red dot) for each of the top openings. A fun question to ask: What is going on physically that gives rise to each of those bifurcations?
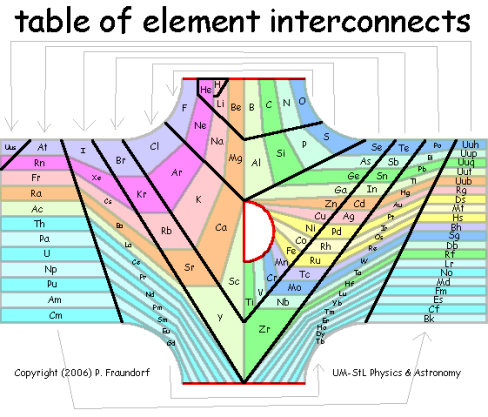

Although the topology of the connections above is dictated by quantum mechanics, the shape and color of each region leaves quite a bit of room for artistic license to address problems like that of flow, color balance, information content, and "crowding for the rare earths". In fact, one might imagine "periodic table shirt" design contests that honor the topological constraints, but go for a variety of effects (both aesthetic and conceptual). They might even work in a junior high school math class, making for a nicely cross-disciplinary experience. Of course, figuring out how to manufacture the contest prize i.e. a shirt without obtrusive blank spots, is another story. Suggestions invited...