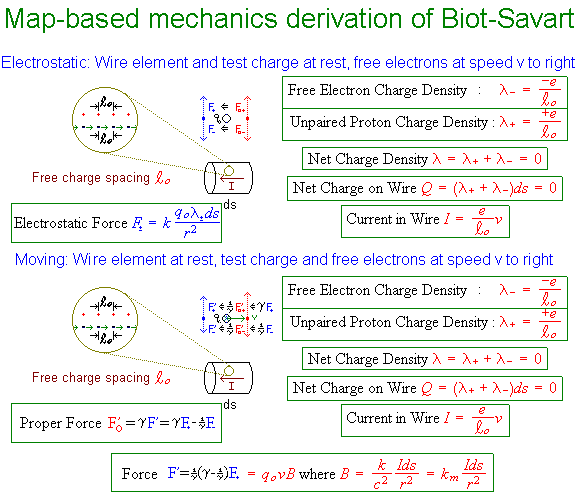
The figure below outlines a derivation which uses frame-invariance of the proper-force Fo (i.e. the proper-acceleration[1] times the rest mass) to derive Biot-Savart (the equation for determining the magnetic field caused by current in a wire element) from the vantage point of forces F experienced in a single frame. When these forces are perpendicular to the line of a test particle's velocity v⊥, proper-force is simply related to the frame-variant force F (defined as usual in terms of momentum and energy transfer) by
Illustrated below are the simplest cases of electric and magnetic forces from a current element, specifically (i) a test charge stationary with respect to a neutral wire carrying an electron current, and (ii) a test charge moving along with the electron current in that wire. For the first case (top half of figure), the forces act on a stationary particle so that v⊥ is zero and γ⊥ is 1. Thus the forces from positive and negative charges in the neutral wire cancel out. Magnetic effects are not seen.

For the case at the bottom on the figure, we again only have to worry about the force perpendicular to the line of particle motion. In this case, the proper-force exerted on our test charge by the stationary positive charges remains in the direction of their separation, but increases in magnitude by that factor of gamma, i.e. Fo+'=γF+.
What the moving electrons do to the test particle as it matches speed with them would be less clear, except that by symmetry the proper-force in that case (Fo-') must decrease by the same factor of gamma, since the test particle now moves with them rather than the protons. In other words, Fo-'=-F+/γ. Thus the original proper-force from the protons is multiplied by (γ - 1/γ) to yield the total , justifying from our perspective the moving test charge's sense that the wire has become positive via length contraction i.e. protons closer together and electrons further apart. Hence the net force F' from the lab point of view is the original frame-variant force from only the positive charges F+, multiplied by (γ-1/γ)/γ or simply by (v/c)2.
One of those v's (hidden in current I) is used to generate the intermediate quantity B (magnetic field) calculated by Biot-Savart, while the other takes up residence in the Lorentz expression for predicting the effect of such magnetic fields on a moving particle. The magnetic field thus allows one to conceptualize a field-structure around the wire, whose forces on any moving charge may be predicted by the Lorentz Law. Biot-Savart and the Lorentz Law, of course, in vector form also work for arbitrary configurations of moving charge not covered by this simple derivation. A slight change in notation exploits this relativistic symmetry even further. The use of proper force here also makes it clear that similar relativistic or "magnetic-force-like" corrections will apply to any "action at a distance" force in flat (3+1)D spacetime.
The derivation above is simpler than the multi-frame derivation below, which however develops the moving charge's perspective more fully. This multiframe derivation is discussed in some detail by Dan Schroeder in his notes here on "Purcell Simplified: Magnetism, Radiation and Relativity".

[1] Proper-acceleration and proper-force are nothing more than the 3-vector acceleration and net force experienced in the frame of an accelerated object. Like proper time and proper length, they describe quantities from the vantage point of a special frame, namely that of the object to which the acceleration and forces apply. Their magnitude also happens to be the Lorentz-invariant magnitude of the net force and acceleration four-vectors as seen from any frame, since in the rest frame of the accelerated object the time-like component of these four-vectors is zero. Because forces might be caused by objects moving with respect to one another, proper forces don't obey an action-reaction principle. The equivalence principle makes these quantities useful even in non-inertial settings (like gravitationally-curved spacetime). The utility of Newton's Laws for describing gravity on earth, along with other inter-object forces, is living proof of that.