
Discover it yourself:
Map-based motion at any speed
This page is one step in a personal journey to discover 20th century methods for describing motion. It is designed like a multiple choice MAZE with challenges along the way that depend a good deal on the strategies that YOU adopt. Although the questions may look simple, they are designed to lead you toward deep understanding quickly. For example, if you think through in your own way the first three challenges in the series, you will have everything needed to derive all kinematic consequences of the special theory of relativity, and put it through some experimental tests as well. Subsequent challenges will draw out consequences for accelerated motion, and even a quantitative look at simple spacetime curvatures, all from the vantage point of a single map-frame before the complications of multiple reference frames are explored.
Imagine a land labeled with a coordinate grid having intersection points at regular intervals of 100 meters, in both x and y directions. A clock is located at each of these intersection points, as in the figure below. Imagine also that you stand at the origin of this map grid at ``time-zero'', and that from your perspective simultaneously all clocks across the land read time-zero as well. In this sense, the map clocks are synchronized. If we further assume that spacetime is not curved by strong gravitational forces, then we can assume that they will stay synchronized as well.
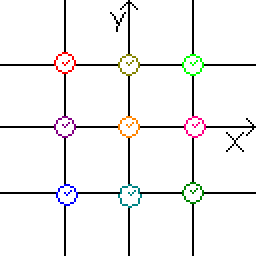
Consider an airplane pilot, flying over this land, who sneezes once in the cabin of his airplane while over the red clock at (x,y) = (-100,100) meters, and again while over the orange clock at (x,y) = (0,0). The pilot's view of some topography on approach (before sneezing) is illustrated below.
Question for YOU: From the vantage point of the pilot, of course, the two sneezes both occur where she is located in the airplane cockpit. But from the vantage point of those sitting around on the map, how far apart in space do the two sneezes occur?
Hint: You might take an experimental approach, and try determining the distance by making measurements on the image at the top of this page. As far as theory that might be of help here, the Greek mathematician Pythagoras comes to mind.
Number of visits here since last reset is  .
.
This Discover-It-Yourself Series is Copyright 1987-1997 by P. Fraundorf,
Department of Physics & Astronomy, University of Missouri - St. Louis.
Send comments and/or questions to pfraundorf@umsl.edu.



