Lorentz from the metric
The Lorentz transformation equations follow simply from Minkowski's space-time version of Pythagoras' theorem, the metric equation. Pythagoras' theorem is for right triangles just "the hypoteneuse squared equals the sum of sides squared", or in other words 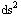= 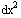+ 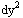. This also works in three dimensions. To get the metric equation, one simply adds in a "side" of length icdt, where c is the speed of light, dt is a time interval measured with respect to the same "map frame of motion" whose yardsticks measured the sides (e.g. dx), and i is the square root of minus one. Since everything gets squared anyways, we get rid of the i's by putting minuses in the right location. Rearranging, for the unidirectional metric equation we get 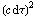= 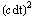- 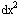= 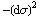. Here c is the spacetime-constant relating time and distance units (often called "lightspeed"), dτ is the proper time elapsed on the clocks of a traveler when dx/dt is less than c, and dσ is the proper distance between two spatially separated events when dx is greater than c dt. One cool thing about the metric equation is that, by tweaking it's "unit coefficients" only slightly, we can make spacetime curve and cause cool stuff like terrestrial and black-hole gravity.
To move to Lorentz transforms, we adapt here the strategy employed by Professor Thomas A. Moore in "Book R" of the excellent McGraw-Hill introductory text "Six ideas that shaped physics". The basic idea is simple. For a time-like interval in the frame of a moving observer (illustrated below by points O and P), one can define relative coordinate-velocity v (of the primed with respect to the unprimed observer) as dx/dt, relative β≡ v/c, and the corresponding relative . Solving the metric equation above for dt in terms of time elapsed in the traveling frame, one gets that c dt = γ c dτ. Solving the metric equation instead for dx, one gets dx = γ v dτ. Try it, and see if you agree. These equations relate to the diagram because, in this case, dτ = dt'.

The equations for time-like intervals in the frame of a moving observer are quite important. For example, they prove that gamma is "speed-of-map-time" dt/dτ from the perspective of the traveler, and that γv is the map-distance traveled per unit traveler-time or proper-velocity w ≡ dx/dτ. These two quantities, with gamma multiplied by c, make up the velocity four-vector which is purely time-like in the traveler frame but takes on space-like components (proper-velocity) as the traveler frame begins moving. Multiply these by rest mass m, and we get components of our traveler's energy-momentum four-vector as well. Since infinity is a reasonable upper-bound on proper-velocity and gamma, c is an upper-bound on coordinate-velocity v.
A similar strategy can be applied to a drawing for spacelike intervals between events simultaneous to a traveling observer (e.g. events lying on the traveler's x'-axis). From the metric equation, one can show that dx = γ dσ, and c dt = γ β dσ. These tell us about the x'-axis interval because, in this case, dσ = dx'. As you'll see from the drawing if you do it yourself, dx' represents the apparent length of a stationary rod of length dx. Since gamma is always greater than or equal to one, the first of these equations means that to a stationary observer the length of moving objects appears contracted in the direction of motion. The first equation in the previous paragraph similarly implies that the time between a traveler's clock-ticks appears dilated (spread out) to someone not moving with them.
These four relationships for time-like and space-like intervals elapsed between events can be applied to events O and Q in the drawing below. It is then simple to calculate the rest-frame space and time intervals (blue) in terms of the space and time intervals (green) experienced by the traveling observer. As you can see from the drawing, in each case a sum of two terms is needed. The resulting "inverse Lorentz transform" equations are c dt = γ (c dt' + β dx'), and dx = γ (β c dt' + dx').

Given the above two equations in terms of two unknowns (dx' and dt'), one can solve for them to get the "forward Lorentz transform" equations. In effect, the sign of beta is reversed, giving: c dt' = γ (c dt - β dx) and dx' = γ (-β c dt + dx). These are illustrated in action measuring the interval between events O and Q, in the x-ct diagram animation below...

Note that the time-elapsed between these two events is shortest to that constant-speed observer,  with β' = 0.6, for whom both events happen at the same place. Further study of these diagrams shows that accelerated observers present at both events experience even shorter elapsed times between O and Q! An extreme example might be a photon of light, emitted by event O, bouncing off a mirror, and returning to be absorbed by event Q. Since gamma is infinite for photons, time on their clocks doesn't pass at all! Ironically, therefore, a principle of extremal aging is also hidden in the metric equation, whereby the straight path between two events takes the most (not the least) time on the part of the traveler. It turns out that this principle works in curved space-time as well.

Created by Mathematica  (November 2, 2004)