Deciding Which Method to Use when Solving Quadratic Equations

When solving a quadratic equation, follow these steps (in this order) to decide on a method:

  1. Try first to solve the equation by factoring.  Be sure that your equation is in standard form (ax2+bx+c=0) before you start your factoring attempt.  Don't waste a lot of time trying to factor your equation; if you can't get it factored in less than 60 seconds, move on to another method.
  2. Next, look at the side of the equation containing the variable.  Is that side a perfect square?  If it is, then you can solve the equation by taking the square root of both sides of the equation.  Don't forget to include a ± sign in your equation once you have taken the square root.
  3. Next, if the coefficient of the squared term is 1 and the coefficient of the linear (middle) term is even, completing the square is a good method to use.
  4. Finally, the quadratic formula will work on any quadratic equation.  However, if using the formula results in awkwardly large numbers under the radical sign, another method of solving may be a better choice.
Now we'll look at some equations and think about the most appropriate method for solving them.
 
 

Example 1: Solve x2 + 4 = 4x

First, put the equation in standard form so that we can try to solve it by factoring:

x2 - 4x + 4 = 0

(x - 2)(x - 2) = 0

x - 2 = 0 | x - 2 = 0

x = 2 | x = 2

So the solution to this equation, found by factoring, is x = 2.
 
 

Example 2: Solve (2x - 2)2 = -4

The side of the equation containing the variable (the left side) is a perfect square, so we'll take the square root of both sides to solve the equation.

(2x - 2)2 = -4

2x - 2 = ± 2i

2x = 2 ± 2i

x = 1 ± i

Notice that the ± sign was inserted in the equation at the point that the square root was taken.
 
 

Example 3: Solve x2 + 6x - 11 = 0

This equation is not factorable, and the side containing the variable is not a perfect square. But since the coefficient of the x2 is 1 and the coefficient of the x is even, completing the square will be an appropriate method. To find the number which needs to be added to both sides of the equation to complete the square, take the coefficient of the x term, divide it by 2, then square that number. In this problem, 6 ¸ 2 is 3, and 32 is 9, so we'll add 9 to both sides of the equation once we have isolated the variable terms.

x2 + 6x - 11 = 0

x2 + 6x = 11

x2 + 6x +9 = 11 + 9

(x + 3)2 = 20


Example 4: Solve 2x2 - x + 5 = 0

This equation is not factorable, the left side is not a perfect square, and the coefficients of the x2 and x terms will not make completing the square convenient. That leaves the quadratic formula as the best method for solving this equation. We'll use a=2, b=-1, and c=5.
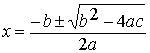