|
|
|
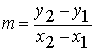 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Some useful information about lines
|
|
|
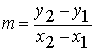 |
|
|
|
|
|
|
|
|
|
|
|
|
|
The most difficult part of working with points, slopes and lines is determining which formula to use when solving specific problems. When you are trying to solve a problem, ask yourself these questions:
The chart below outlines the methods that are appropriate
to use when solving specific types of problems.
|
|
|
|
| Slope of a line | Coordinates of two points on the line | Use the slope formula |
| Slope and y-intercept of a line | Equation of a line in standard form | Write the equation in slope-intercept form |
| Equation of a line | Slope of the line and a point on that line | Use the point-slope formula |
| Equation of a line | Slope and y-intercept of a line | Use the slope-intercept formula |
| Equation of a line | Coordinates of two points on the line | Use the slope formula to find the slope of the line, then use the slope and one of the points in the point-slope formula |
| Equation of a line parallel to a given line | Equation of the given parallel line and a point on your line | Write the equation of the given line in slope-intercept form to determine its slope, then use that same slope and your point in the point-slope formula |
| Equation of a line perpendicular to a given line | Equation of the given perpendicular line and a point on your line | Write the equation of the given line in slope-intercept form to determine its slope, then use the opposite reciprocal of that slope and your point in the point-slope formula |
Let's look at some examples.
Example 1 What is the slope of a line through the points (2,3) and (4,-5) ?
What do we already know? Two points on the line
What method will we use? Use the slope formula
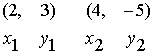
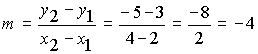
Example 2 What are the slope and y-intercept
of 2x - 3y = 5 ?
What do we already know? The equation of a line in standard form
What method will we use? Write the equation in slope-intercept form
2x - 3y = 5
- 3y = - 2x + 5
y = 2/3 x - 5/3
Since the equation now is in y = mx + b form, we can identify the slope m=2/3 and the y-intercept b=-5/3
Example 3 What is the equation of a line with
slope - 2 which passes through (3,-5)?
What do we already know? The slope and a point on the line
What method will we use? Use the point-slope formula
m = -2, (x1, y1) = (3, -5)
y - y1 = m(x - x1)
y - -5 = -2(x - 3)
y + 5 = -2x + 6
y = -2x + 1
Example 4 What is the equation of a line with
slope 3/4 and y-intercept - 3?
What do we already know? The slope and y-intercept
What method will we use? Use the slope-intercept formula
m = 3/4, b = -3
y = mx + b
y = 3/4 x + -3
y = 3/4 x - 3
Example 5 What is the equation of a line that
contains the points (3,4) and (1,-2)?
What do we already know? Two points on the line
What method will we use? Use the slope formula to find the slope of the line, then use the slope and one of the points in the point-slope formula
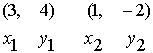
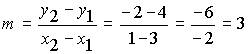
Now use one of the points and our slope in the point-slope formula:
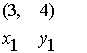 m
= 3
m
= 3
y - y1 = m(x - x1)
y - 4 = 3(x - 3)
y - 4 = 3x - 9
y = 3x - 5
What do we already know? A point on our line and the equation of a line parallel to our line
What method will we use? Write the equation of the given line in slope-intercept form to determine its slope, then use that same slope and your point in the point-slope formula
3x - y = 5
- y = - 3x + 5
y = 3x - 5
m = 3, b = - 5
So the slope of the given line is 3
Parallel lines have equal slopes, so the slope of our line is also 3. Our line also goes through the point (-1,4), so we'll write an equation with the point-slope formula.
y - y1 = m(x - x1)
y - 4 = 3(x - - 1)
y - 4 = 3(x + 1)
y - 4 = 3x + 3
y = 3x + 7
Example 7 Find the equation of the line through
(4,-1) that is perpendicular to 4x+3y=2
What do we already know? A point on our line and the equation of a line perpendicular to our line
What method will we use? Write the equation of the given line in slope-intercept form to determine its slope, then use the opposite reciprocal of that slope and your point in the point-slope formula
4x + 3y = 2
3y = - 4x + 2
y = - 4/3 x + 2/3
m = - 4/3, b = 2/3
Perpendicular lines have slopes that are opposite reciprocals, so the slope of our line is the opposite reciprocal of -4/3, or 3/4. Our line also goes through the point (4,-1), so we'll write an equation with the point-slope formula.
y - y1 = m(x - x1)
y - - 1 = 3/4(x - 4)
y + 1 = 3/4 x - 3
y = 3/4 x - 4